Just for Functions

This school year our first cohort of IB students began working its way through the junior year of their two-year course of study. One of the things I’ve found interesting about the experience is teaching with international materials and textbooks published outside of the United States, and seeing how different countries might approach some of the same knowledge. There’s been some slightly new vocabulary to adjust to, and some idiosyncratic decisions when it comes to what is and what isn’t part of the curriculum.

[Tangent—feel free to disregard unless you’re a nerd like me—For example, as far as I can tell, the IB never makes reference to the secant, cosecant, and cotangent trigonometric ratios. My first thought on seeing that was, Good. Those just provide more opportunities for kids to get confused, they’re not present on the TI-84, and they add virtually nothing to the study of trigonometry. But then my calculus-teacher brain kicked in and said, What’s the derivative of tan x then? So I flipped through an IB textbook to see if they continued to avoid the reciprocal functions even then. They do: (d/dx) tan x = 1/cos²x.  ]

One of the neat things about this has been that when you ask old questions in new ways, sometimes you stumble across some interesting results. A few weeks back, a test for IB Mathematics SL students which I created using real, released questions from actual IB exams, relied on the students being able to answer the following:

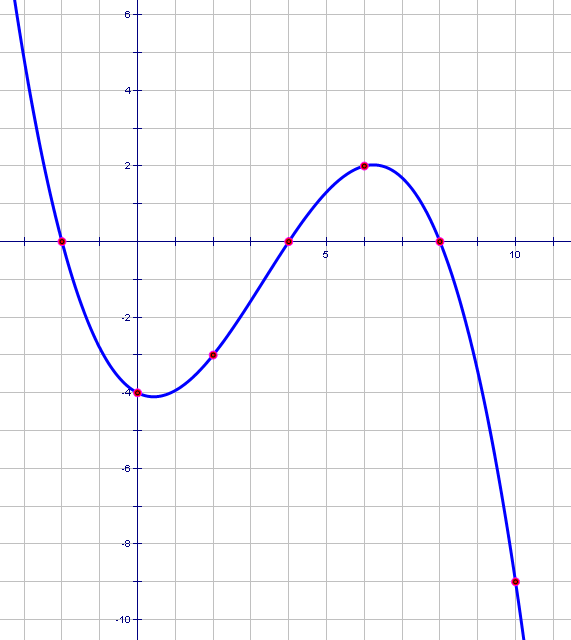
f (2) = _____       f (6) = _____       f (-2) = _____       f (0) = _____       etc.

This wasn’t actually the material being tested—and it’s not directly part of the IB curriculum but rather a prerequisite—but basically, the students would need to know how to answer those questions to answer the questions they were actually being asked.

For perspective, the students in this course have all completed Honors Algebra 2, and some of them have completed Honors Precalculus as well.

Now knowing my readership, at this point half of you are thinking to yourself, That’s a stupidly easy question. Why are you even talking about it? The other half are thinking Ouch! I became a writer because I hate math! Now you made my brain hurt! Either way, relax.

(If you’re very confident with math, you may want to skip the next paragraph.)

If you’ve not looked at math in decades and you don’t remember what the symbolism means, then just take it on faith that this line of questioning should be trivial. If you’re not sure but you’re curious to know what the kids were supposed to do, remember that every point on a coordinate plane has two coordinates, an x-coordinate and a y-coordinate. Listing the coordinates in order gives the “address” of any particular point, kind of like when you played Battleship as a kid. As for the question itself, kids are told from Algebra 1 on (if not sooner) that f (x) is another way of saying y. Even though it contains the letter x, it means y. The reason it contains the letter x is to make it possible to talk about specific values of y that go with specific values of x. So if I ask, “What does  f (10) equal?” I’m asking students to find the point where x = 10, and tell me what that point’s y-coordinate equals. So I’ll put the answer to the question here in white, and you can highlight it with your mouse to see if you understood what I meant. f (10) = -9. This represents the lower right dot on the graph, the point (10, -9).

Students in an honors math class ought to know this, but—and this is the important part—this isn’t how we usually ask the question. Usually instead of giving students a graph, we do the more “advanced,” algebraic thing, and we define the function using variables. So we might say that f (x) = (x³ – 10x² + 8x + 64)/(-16). Then we might ask, “What is f (4)?” The kids, having been trained in the proper algorithm to follow, will “plug in” 4 wherever they see x, and find that:

f (4) = (4³ – 10 • 4² +  8 • 4 + 64) ÷ (-16)

= (64 – 160 + 32 + 64) ÷ (-16)

= 0 ÷ (-16)

= 0

And we’ll feel good about this as teachers, because they’ll have answered the “harder” question. Wouldn’t you agree that what I just demonstrated was much more work than simply looking up the point on the graph with an x-coordinate of 4, and seeing that its y-coordinate was 0? We’re making the kids work harder, ergo we’re being more rigorous.

Except . . .

Except that when a question like the above came up on a test for my rather advanced students, most of them could not accomplish the relatively trivial task of looking up function values from the graph itself. Then, on a hunch, I asked my Honors Algebra 2 students, and they could not, by and large, either.

What this says to me is that we have succeeded in teaching a rote process, but failed to teach the concept behind the process. Anybody who knows me knows that this sort of thing is a big deal to me. I am constantly stressing in my classes how important it is to focus on why things work a certain way, sometimes to the frustration of those of my students who would just rather I gave them an algorithm to memorize already. Because there’s the rub: memorizing and plug-and-chug may be more tedium, but they’re actually easier than really getting around why things work.

I suspect, deep down, that we educators are often guilty of conspiring with our students to give them the easy way out. Because happy students are students who don’t complain. So we’re all too happy to settle for the appearance of hard work, rather than the reality of wrestling with a concept from all angles.

Another issue is probably our tendency to adopt curricula that is a mile wide and an inch deep–once again, because it gives us the comforting appearance of rigor. When you have three dozen topics to “cover”—and isn’t “cover” a poor synonym for “teach”?—then who has time to approach the same topic from multiple angles? Who has time for high level questioning?

If you’re a math teacher and you happen to stumble across this page while doing a google search for functions or for graphing or something, do me a favor: give the above problem to your kids, say, as a random bellwork problem. Did it seem trivial to you? Were you certain your kids would breeze past it? Did your students surprise you by struggling with it? Please let me know—I’d love to hear some other teachers’ experiences with this.